Nearly 40 years ago, in 1982, the first CDs were released. It’s hard to believe it has been that long. I should know. I was there. Many of you were not even born then, and you may have never seen what CDs eventually replaced: Vinyl LPs. (It is ironic that LPs have come back with a vengeance, with sales increasing every year at an explosive rate.)
At that time, music studios recorded in the same format that was put onto the CDs that were sold: 16 bit 44.1 kHz (16/44.1) sampling. The Analog-to-Digital Converters (ADCs) used to record music were 16/44.1, and the Digital-to-Analog Converters (DACs) were 16/44.1 as well.
Telarc was a very important pioneer in this field, using 50 kHz for the sampling frequency of their studio masters instead of 44.1 kHz. Some of their recordings were later released in SACD format, using the 50 kHz masters. They did not compress the loud sections of the music like many other studios did, so one had to be very careful when listening to their CDs, to keep their speakers from flying into orbit.
Just like HDTVs have increased their resolution from 1080i to 4320p (it will be erroneously called “8K” – now available in Japan), audio recording of music has also increased its resolution, with at least one company, 2L in Norway, marketing music downloads in 24/352.8
However, high resolution music downloads are only a very small part of the music industry.
Studio recording involves many more tracks than the two stereo tracks that are on CDs. A symphony orchestra may use a dozen microphones to record the various instrument sections, and in this case, there would be twelve tracks in the Digital Audio Workstation (DAW) software that are down-mixed to a two- (stereo) channel CD. A rock band may have five instruments and a singer. They often come into the recording studio at different times and record their parts in songs for an album. Some of the instruments might be recorded in stereo, and the singer, perhaps, using one microphone. So, again, there would be a lot of tracks that are down-mixed to the two-channel CD.
There are several multi-track software programs that are used to edit and manage the numerous audio tracks, with Pro Tools being the most sophisticated (and the most expensive).
There is also a free music track editor, called Audacity, which is very good, even though its capabilities are limited.
In the final down-mix of all the recorded tracks, let’s say recorded at 24/96 sampling, to create a final, two-channel 16/44.1 Redbook CD, there is an artifact called quantization error. (Quantization errors are also in the original 24/96 tracks.)
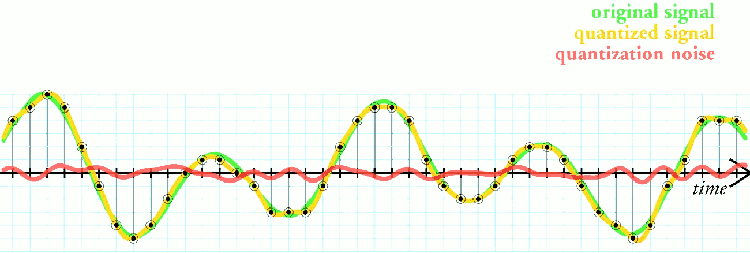
Here is a diagram from Wikipedia (see the “Quantization” link in the Sources listed at the bottom of this article).
Wikipedia states, “The simplest way to quantize a signal is to choose the digital amplitude value closest to the original analog amplitude. This example shows the original analog signal (green), the quantized signal (black dots), the signal reconstructed from the quantized signal (yellow) and the difference between the original signal and the reconstructed signal (red). The difference between the original signal and the reconstructed signal is the quantization error and, in this simple quantization scheme, is a deterministic function of the input signal.”
The quantization errors that were in the original 24/96 tracks are exacerbated in the down-mix to 16/44.1 audio file that would be used for issuing a CD. The reason that the quantization errors are worse are (1) the resolution of a 16 bit file is only 1/256 that of a 24 bit file, and (2) the noise will dither the original conversion to 24 bits quite effectively, but it may be too small to dither conversion to 16 bits well.
Note that all of the digital WAV files (except where indicated) that I have used for this article are synthesized digitally and analyzed in the digital domain, that is, without using a DAC. I did this so that no compounding artifacts from the DAC’s analog output stage are introduced, which would otherwise interfere with showing the full extent of the non-dithered or dithered noise floor. This is the main reason that the noise floors in the spectra shown here are so low.
Even the best DACs can resolve only 22.5 bits out of 24 bit sound files. Analyzing 24 bit sound files in the digital domain, rather than after the sound files have passed through a DAC, allows the full 24 bits to be resolved, giving us a much clearer picture of what digital audio is capable of, and what it is not capable of.
I asked John Pattee, the programmer who created SpectraPLUS, which is what I used to show the spectra in the tests for this article, to explain the noise floor in digital files that are analyzed in the digital domain.
Secrets Sponsor
Here is what he said:
“If you post process an existing WAV file, or play it the recorder mode, the analyzer operates on the digital data values in the WAV file – the sound card is not involved.
A 24 bit WAV file has a theoretical resolution of 224. If a WAV file is built from a purely mathematical algorithm, then the DAC/ADC converters are not involved, and the spectrum is void of any noise issues from the converters.
If the mathematical WAV file contained all zeros, the noise floor would be minus infinity – our plot would show -999 dB.
If the mathematical WAV file contained a 1 kHz pure tone, the spectrum would have a peak at 1 kHz, but the noise floor would depend on a number of factors.
If the frequency of the pure tone is an exact ratio of the sampling rate and FFT size, then the noise floor would be -999 dB. For example:
Sampling Rate: 32768
Tone Freq: 1024
FFT Size: 16384
Smoothing Window: Uniform
What happens in such an example is that the FFT samples are exactly aligned and start and stop at the zero crossings of the sine wave. Because this is rarely the case, smoothing windows are used. Here is a link to more info regarding smoothing windows.
Another issue is that this mathematically pure tone must be converted to integer values for the WAV file (required by the WAV file format). This means that these floating point values are rounded to the nearest integer, and this produces what is called “quantization noise”. These are very small with a 24 bit integer but can be correlated and appear as low level distortion.
A technique called “dithering” is used to cause these rounding errors to be randomized. There are a number of dithering algorithms that control the distribution of this quantization noise.
What all this means is that there will still be a noise floor in the spectral data plot even with mathematically generated tones. It can be lower than the theoretical -144 dB for a 24 bit depth in many cases.”
Basically, dither is white noise, which means that it is random noise at all frequencies within the range of a specific sampling frequency. So, for 16/44.1, the random frequencies range from 0 Hz to 22.05 kHz. For 24/96, the random frequencies range from 0 Hz to 48 kHz. Note that the spectra I show in this article use only single sine waves (1 kHz) for the tests. Dither works for music files that have hundreds or thousands of frequencies, and so does noise shaping (which is discussed later). For this article, I used two DAW (Digital Audio Workstation) software programs: Audacity, which is a free download, and Adobe Audition.
There are several types of dithering, and the most commonly used type is “Triangular”, which minimizes noise modulation. Dithering makes the quantization error larger (on average by 4.77 dB for triangular dithering), but also makes it much more well-behaved. I used triangular dither for all dithered spectra in this article.
Here is a downloadable WAV file of white noise recorded at 16/44.1 and minus 50 dB. Make sure your music player has the sound turned down before you download the sound file. As the sound file plays, you can slowly turn the volume up to a comfortable level.
For the bench tests, to start out, here is an undithered 16/44.1 spectrum (Figure 1, below), using a 1 kHz sine wave as a test frequency. The Y axis shows dBr, which means dB relative to a reference. In this case, the reference is 0 dBFS, which is the loudest signal voltage (loudest sound) that can be recorded without clipping.
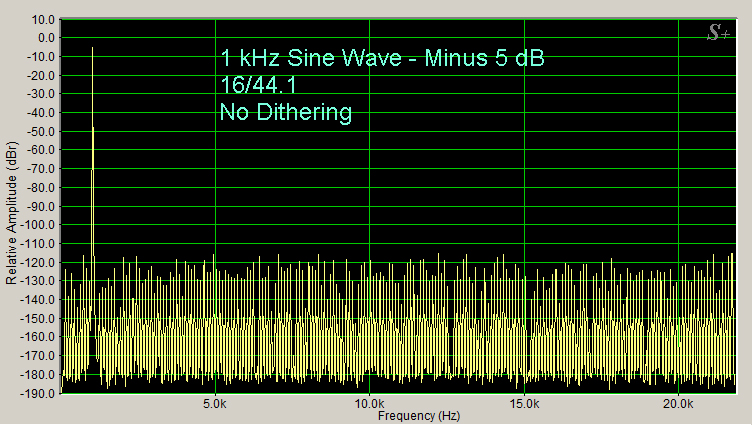
Figure 1
Notice the quantization error distortion spikes.
Here is the same spectrum (Figure 2), but windowed at 20 Hz to 2 kHz to show the details of the quantization error distortion spikes. Note that they occur below the 1 kHz sine wave test frequency as well as above it.
You can see that the quantization error distortion spikes are at 100 Hz intervals. This is the beat frequency (greatest common divisor) of 1 kHz and 44.1 kHz, and it is not white noise. Here is a WAV file of the quantization errors at 100 Hz intervals. Again, be sure to turn down your music player volume before downloading the file. Then turn it up slowly to a comfortable level when listening.
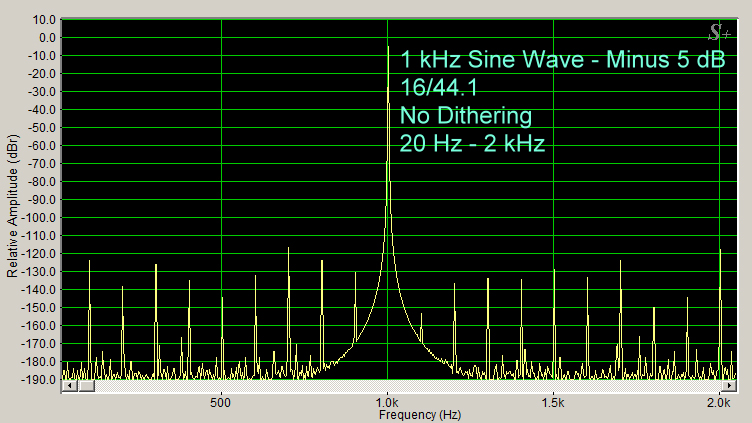
Figure 2
You would never encounter undithered 16/44.1 music (Redbook CD format) because of these quantization error distortion spikes. All Redbook CDs contain dithered 16/44.1 music. Here is a spectrum (Figure 3, below) of a 1 kHz, 16/44.1 signal that has been dithered.
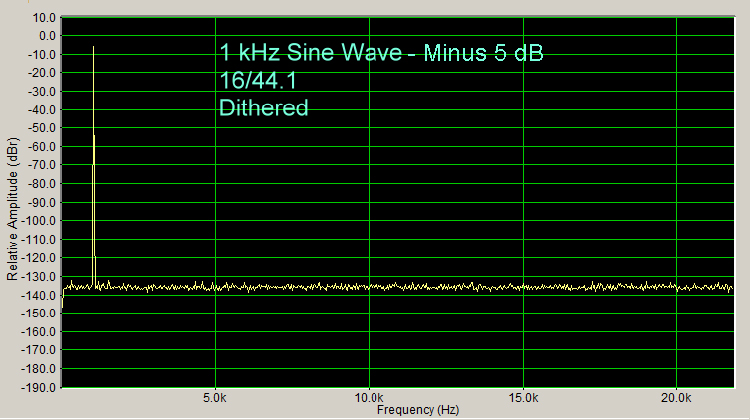
Figure 3
The quantization error distortion spikes are gone. It seems counter-intuitive to add noise to reduce distortion, but that is what happens with dithering.
WAV files that have digital silence (e.g., 16/44.1 with no test tones) do not have any quantization error distortion spikes, because there is no frequency signal, e.g., 1 kHz, that would otherwise beat against the sampling rate, e.g., 44.1 kHz.
Shown below is a spectrum of a 1 kHz sine wave (Figure 4), recorded natively at 24/96 and at minus 5 dB, with no dithering.
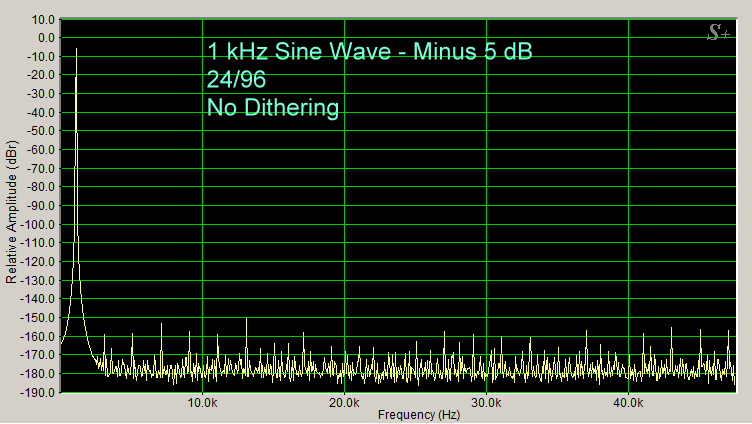
Figure 4
The dithered 24/96 spectrum (Figure 5, below) shows that the peaks have been lowered, but even the undithered 24/96 quantization error peaks (Figure 4, above) are lower than minus 150 dB.
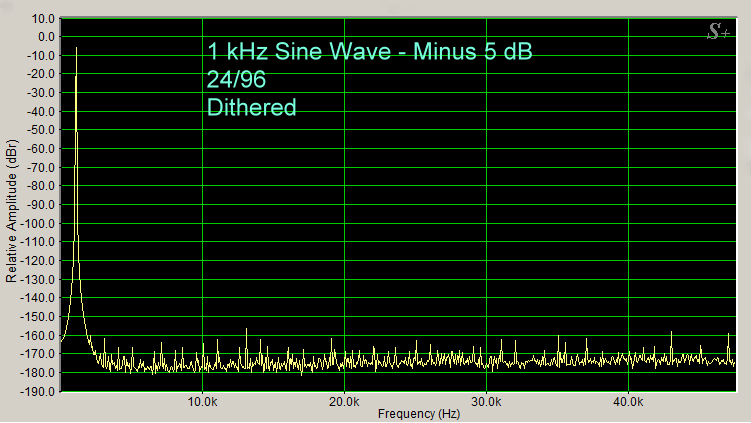
Figure 5
This would suggest that 24 bit depth music files don’t necessarily require dithering. However, dithering 24 bit files is a good idea anyway. Marcel van de Gevel, in the Netherlands, explains this as well as the mathematics of why the peaks in the 16/44.1 undithered spectrum are spaced at 100 Hz:
“Practically, when you have a 24 bit recording of acoustical music, it is unlikely that you need to dither because the analog noise will usually dither things quite well. Besides, if there are any quantization error peaks generated, they will have a very low level. Still, it is good practice to use dither anyway so you don’t have to worry about purely electronic music or about what precisely happens with the probability distribution or the spectral properties of the recorded analog noise along the signal chain.
Secrets Sponsor
Regarding the mathematics of the 100 Hz peaks in the 16/44.1 spectrum, imagine you put your sine wave into a hypothetical noiseless ADC (Analog-to-Digital Converter) that first quantizes its input signal and then samples it. It is easy to see that (for a given sample rate and step size) this gives the same output signal as a noiseless ADC that first samples and then quantizes.
The quantized but not sampled waveform in our hypothetical ADC is simply a distorted sine wave. That is, its period time is exactly the same as that of the input sine wave, but it is staircase-shaped rather than perfectly sine shaped. Hence, it has harmonics at multiples of the frequency of the original sine wave. If the input-to-output relation of the quantizer is an odd function, the distorted sine wave will have a symmetrical waveform that only consist of odd harmonics (see Section 3 of “Even and Odd Functions” in the Sources listed at the end of this article).
After sampling, the higher harmonics may alias to different frequencies. When the sample rate is an exact integer multiple of the frequency of the distorted sine wave, the aliases all still fall on integer multiples of the frequency of the distorted sine wave.
This is not the case when the sample rate is not a multiple of the frequency of the distorted sine wave. When both are integer multiples of some beat frequency fbeat, all aliases have to be on exact multiples of this beat frequency. Both the distorted sine wave and the sample rate have then had an exact integer number of periods after a time 1/fbeat, which means that the quantized and sampled signal will repeat at least every 1/fbeat. Hence, the quantized and sampled signal will be periodic with a period time of (at most) 1/fbeat, and will therefore only have harmonics at multiples of fbeat.”
So, what about the time domain of a 16/44.1 undithered signal at minus 90 dB? Here is a 1 kHz waveform at minus 90 dB (Figure 6, below) from my reference DAC, the AURALiC VEGA. This is an analog waveform, meaning that the 1 kHz, 16/44.1 signal was generated as a digital signal by an Audio Precision, then fed to the AURALiC VEGA DAC, which converted it from the digital signal to an analog signal, and the analog signal was then fed back to the Audio Precision for analysis.
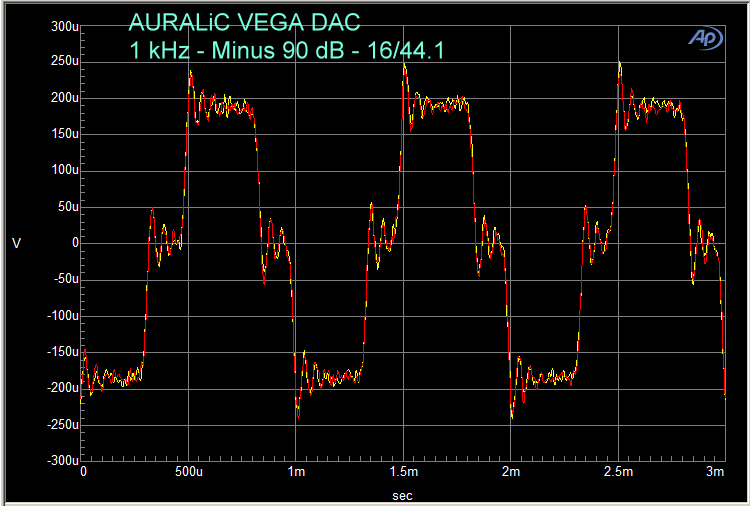
Figure 6
You can see that each sine wave has four samples, with the positive and negative peaks at + 200 microvolts (µV) and – 200 µV respectively, but the waveform has characteristics of a square wave, which means there are numerous additional harmonic distortion peaks. There are some very low level sine waves mixed in with the 1 kHz wave. These are distortion peaks which are removed by dithering.
If we use 24 bits instead of 16, but keep the sampling frequency at 44.1 kHz, the square wave characteristics are gone (Figure 7, below).
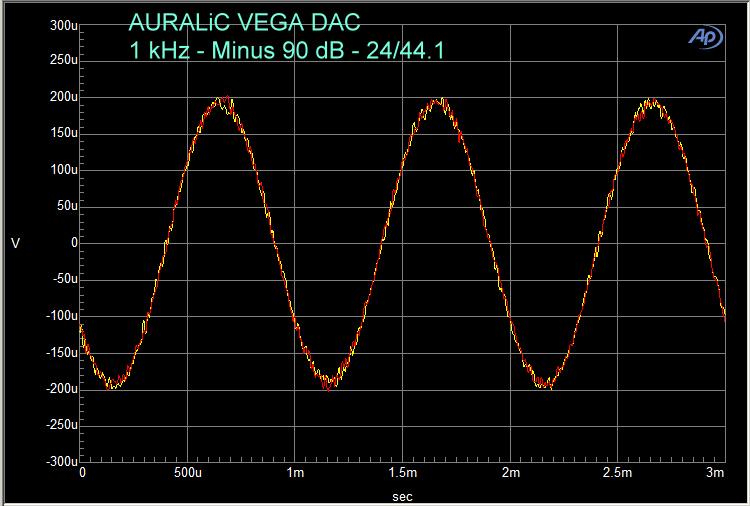
Figure 7
This means that the bit depth is critical to reproducing the sine wave without harmonics at low level signals. This occurs because, at 16 bits, there are 216 (65,536) possible voltages to be represented by samples. At low signal levels, there are only a few available voltage values to characterize the sine wave. With a 24 bit depth, the voltages that are possible are 224 (16,777,216). So, at low levels, there are 256 more possible voltage samples available than there are with a 16 bit depth. This is enough to easily characterize a complete sine wave at minus 90 dB.
In running further tests, I found that changing the bit depth from 24 bits to 16 bits, regardless of the original sampling frequency, and saving the file without dithering, produced quantization errors, so in the case of down-converting audio files to 16 bits, dithering should always be used.
The bottom line here is that dither really works beautifully to eliminate quantization errors when the original music file is 16 bits or when down-converting 24 bit files to 16 bit files.
Noise shaping is a second method to improve the digital audio that consumers listen to. What it does is lower the noise floor in one place (the audio spectrum; 20 Hz – 20 kHz), and move the noise to another place (out of the audio spectrum), and is accomplished using feedback, as opposed to adding white noise to produce dithering. Noise shaping is usually applied, along with dither, when down-mixing numerous tracks to stereo and down-converting to the final sampling frequency and bit depth.
To illustrate noise shaping, I have synthesized some test tones and down-converted them to a lower sampling frequency and bit depth, using two different examples.
Noise shaping can be applied within the audible spectrum if desired. So, Figure 8, shown below, is a spectrum of a 1 kHz, 24/96 WAV file converted to 16/44.1, with dithering and with noise shaping, using 16 kHz as the crossover point (the beginning of the place where the noise shift increase is located).
Notice that the effects of quantization errors have been eliminated as previously shown in the Dithering section of this article, and the noise floor has been reduced from about 600 Hz to 16 kHz by as much as 15 dB, with the noise shifted to the region of 16 kHz to 22 kHz, so that it is as high as minus 110 dB (remember that with the 16/44.1 spectrum with dithering but no noise shaping, the noise floor is at minus 135 dB – see Figure 3). The increase in the noise level in Figure 8 to minus 110 dB, beginning at 15 kHz in the noise shaped spectrum, would still be inaudible.
The noise shaping that I used is “Heavy, Weighted”, with the word “Heavy” meaning that the noise shaping is very intense, and the word “Weighted” meaning that the region from about 3 kHz to 8 kHz is where the noise shaping mostly occurs (has the lowest noise floor), because this is the region where the human ear is most sensitive.
There are numerous types of noise shaping, just as there are numerous types of dithering. I used Heavy, Weighted to make the changes obvious.
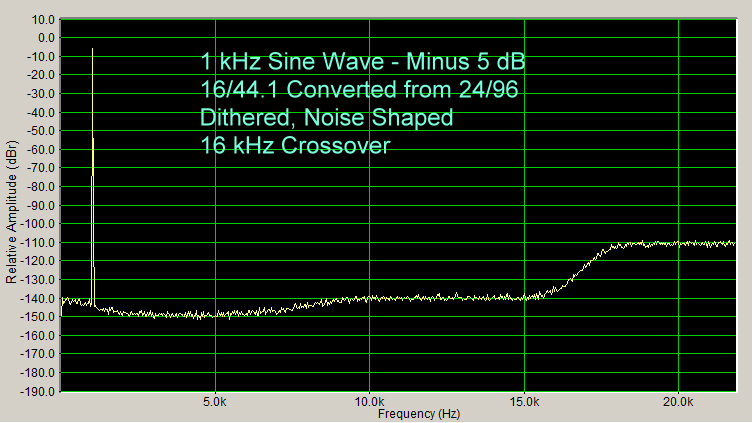
Figure 8
Noise shaping can also be applied to high resolution WAV files.
Below (Figure 9) is a spectrum of 24/192 sampling, converted to 24/96, with dithering and noise shaping, using a crossover frequency of 40 kHz.
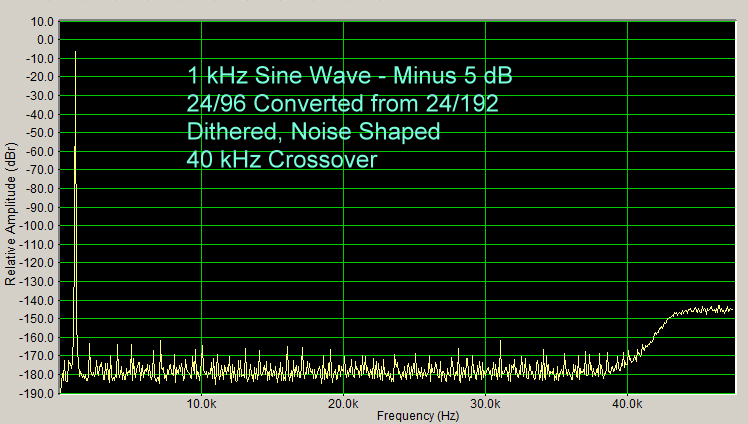
Figure 9
It made a slight, but noticeable improvement compared to the 24/96 spectrum that has been dithered but not noise shaped (see Figure 5, above).
The bottom line on noise shaping is that it works better with 16/44.1 WAV files than high resolution WAV files, but it is likely to be used with high resolution WAV files if there is additional digital signal processing during the mastering stage that raises the noise floor.
For SACD, which is a 1 bit delta-sigma CODEC, noise shaping is absolutely necessary, because a 1 bit depth yields a noise floor at only minus 6 dB (there is 6 dB lowering of the noise floor for each bit in the sampling).
Noise shaping lowers the SACD noise floor to a level similar to multi-bit PCM. Figure 10 (below) shows an example spectrum from an SACD test disc, using an OPPO BDP-105 universal player decoding it as DSD to an analog signal, which was fed to the Audio Precision for analysis.
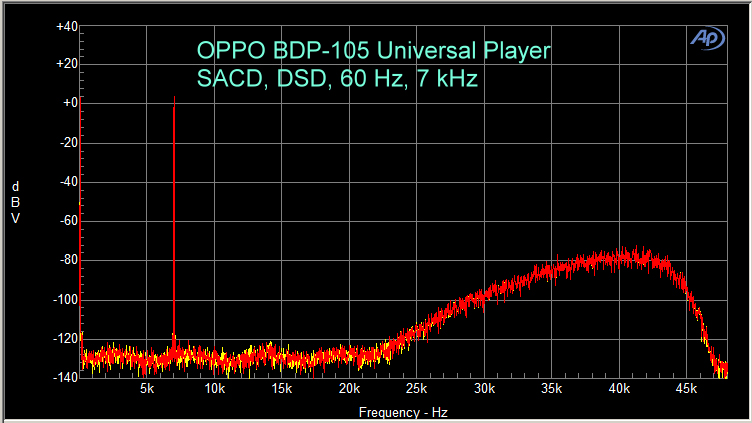
Figure 10
You can see that the noise shaping crosses over just above the audible band at around 22 kHz. The noise at 40 kHz is minus 72 dB, which would be audible if it were in the audible band, but at 40 kHz, we cannot hear it. The noise floor here is higher than 24/96 PCM spectra shown in other parts of this article because the signal shown here has passed through the OPPO BDP-105’s DAC, and then the analog output of the DAC has been passed back into the spectrum analyzer. The other spectra (Figures 6 and 7 are waveforms, not spectra) are from digital WAV files maintained in the digital domain for analysis and do not pass through a DAC, becoming analog signals.
Well, I hope you were not overwhelmed with all the spectra, but I could not find any article on the Internet that explained dithering and noise shaping in a straightforward manner, so I felt it would be helpful to do that here at Secrets.
I contacted two mastering studios, and was told that most music files created by recording studios and sent to them for mastering (mixing, balancing the various tracks to specific volume, and adding special effects, such as reverberation) were at 44.1 kHz and that most of those were 24/44.1 kHz. This means that some of the files were 16/44.1. Therefore, most music sent from recording studios to mastering studios are meant to be finalized at 16/44.1.
This puts audiophiles who want high resolution music downloads or streaming in a conundrum. How can we get high resolution music if it is now being recorded mostly at 44.1 kHz sampling frequency? Up-converting the files to 24/96 or 24/192 won’t do the job. It has to be native 24/96 or 24/192 to be considered high resolution.
On the other hand, perhaps the mixing companies could create two products from the 24/44.1 master files sent to them by recording studios: (1) a down-mix to 24/44.1 stereo for streaming, maintaining the native 24 bit depth; and (2) a 16/44.1 down-mix for CDs.
Native 24/44.1 would have all the advantages of a large dynamic range characteristic of 24 bit files (meaning you would hear more low-level detail), and also it would carry the full audible spectrum (20 Hz – 20 kHz). It would have a very small bit rate for streaming, assuming the mixing studios use FLAC lossless compression. This would insure no dropouts that characterize high bit rate music files (e.g., 24/96). There would be no need for further processing by the streaming companies to reduce the file size.
“Dithering Explained: What it is, When to Use It, and Why it’s Important”
“When and to what should I apply dithering?”
“Compact Disc” (When CDs first Came Out)
“Do I really need to use dithering?”
“The Mathematics of Dithering and Noise Shaping”
“The Super Audio CD (SACD) – DSD – DXD”
Acknowledgments: The author wishes to thank Nelson Pass, John Pattee, Jan Didden, Marcel van de Gevel, and David Rich for their assistance in the preparation of this article.