Let’s do a Spice Simulation of this design.
Spice Simulations of a two-way, 2nd-order Speaker Crossover Network with an Assistance Part that is Not in the Signal Path.
| Assistant Part | In Simulation? |
Function in the Graphs |
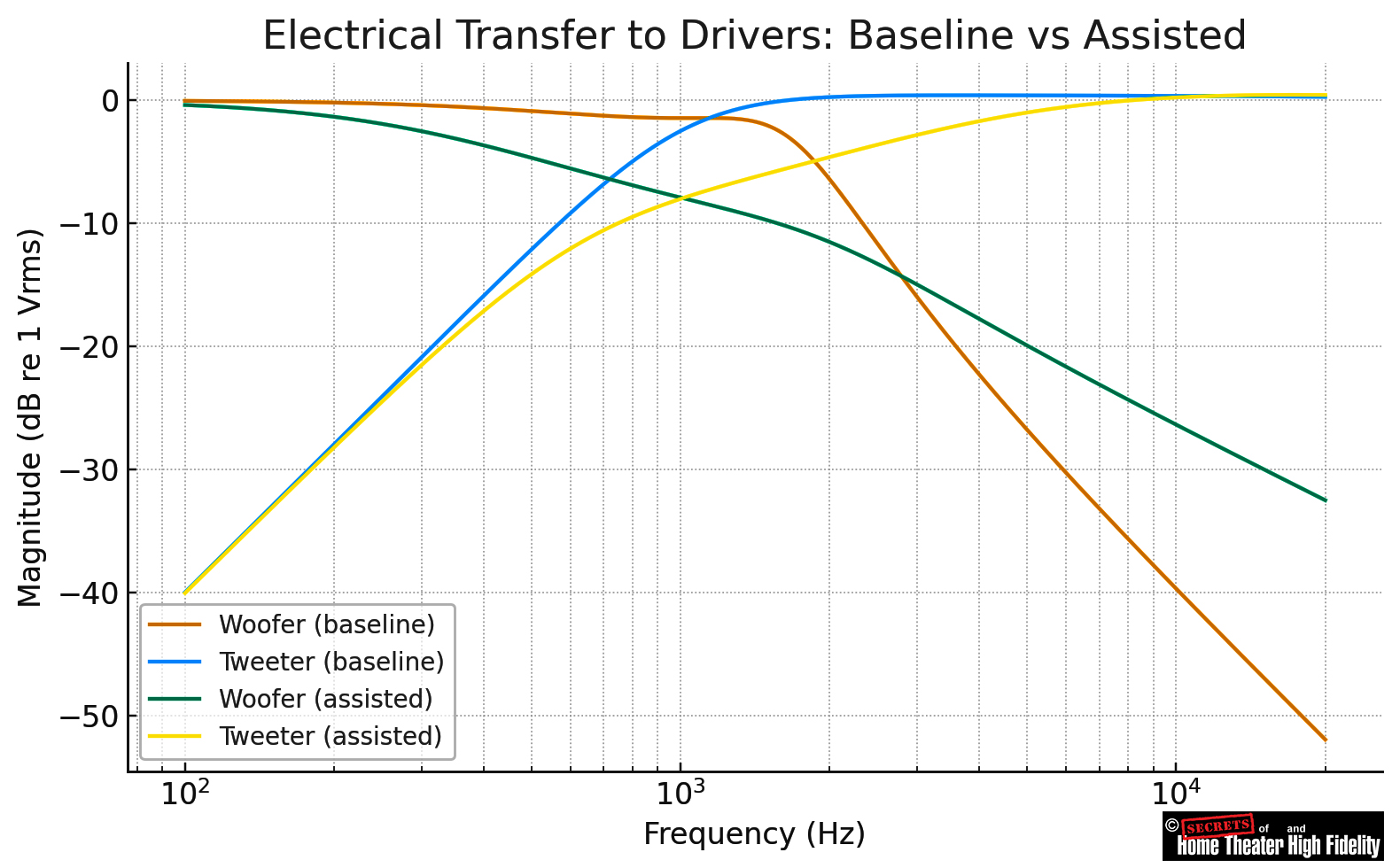
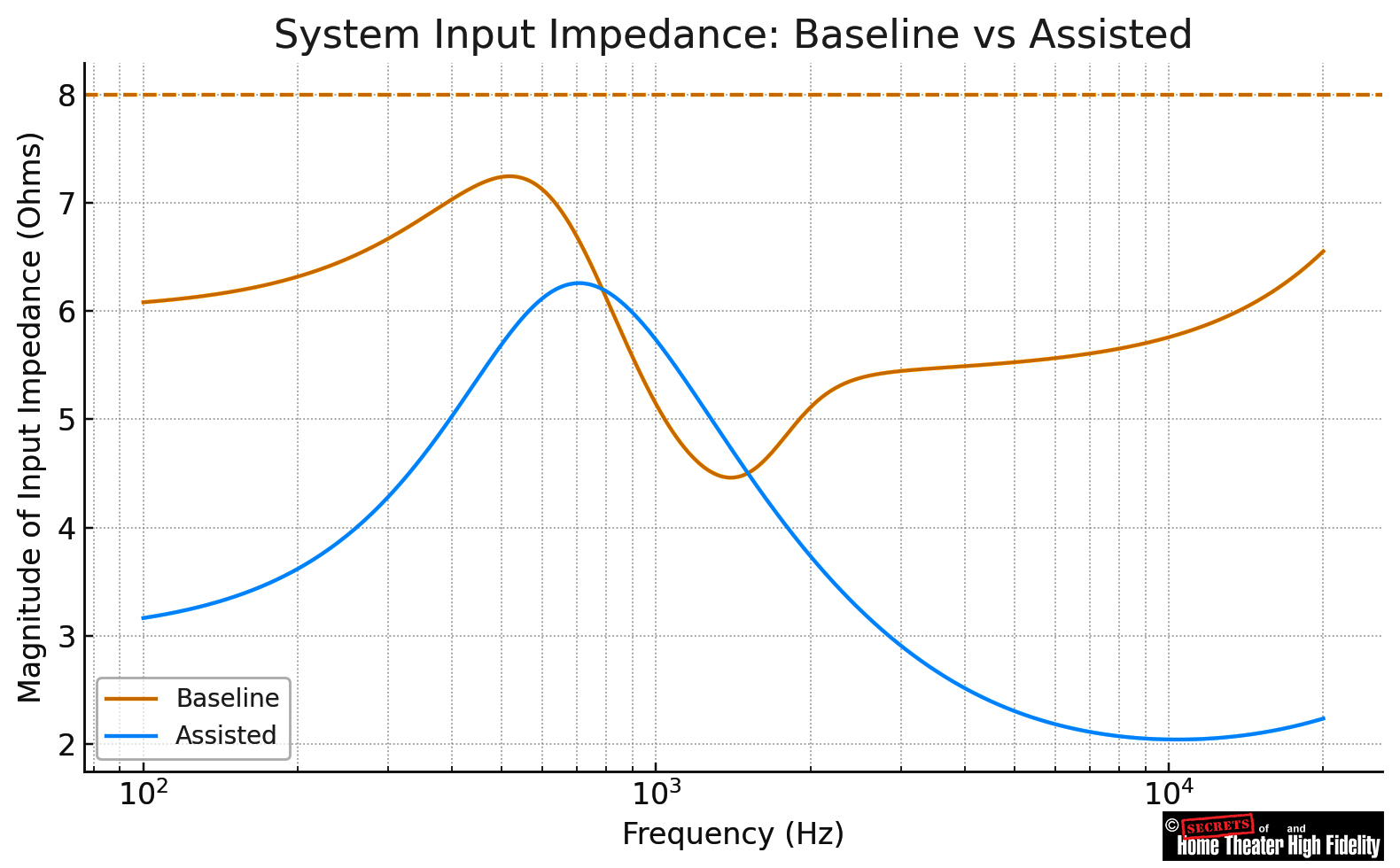
| Woofer Zobel (Rz ∥ Cz) | Yes | Flattened the woofer’s rising impedance; in your impedance plot, you can see a smoother, less inductive high-frequency slope. |
| Tweeter LCR notch (series L–C–R) | Yes | Suppressed the small high-frequency bump in the tweeter curve around 6 kHz in the Electrical Transfer graph. |
| RC damper across the woofer series inductor (Rd ∥ Llp) | Yes | Slightly reduced the overshoot of the woofer’s electrical slope near the crossover (~2 kHz) and removed a small resonance in the impedance trace. |
| Tweeter shunt resistor (Rsh across tweeter) | Yes | Stabilized the tweeter branch’s impedance above crossover; the “assisted” impedance curve stays closer to 8 Ω instead of rising sharply. |
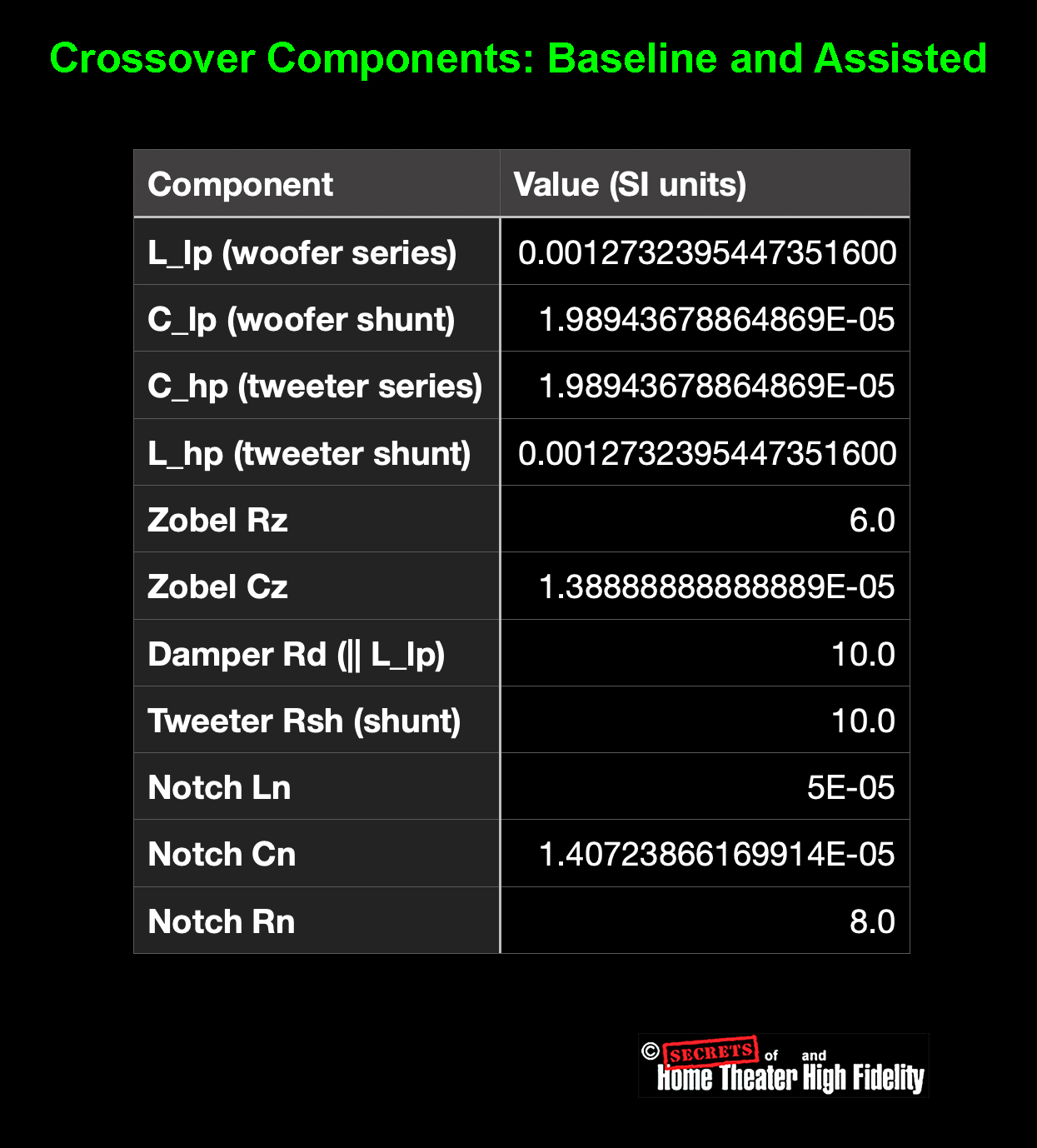
The table above is a component summary for the simulated two-way crossover network used to generate your original graphs. It lists all electrical elements in both the baseline (standard LR2) and assisted versions of the crossover, along with their exact numeric values in SI units (henries, farads, and ohms).
Secrets Sponsor
Here’s what each section represents:
Main crossover filter (baseline)
| Component | Function |
| L_lp (0.00127 H) | Series inductor feeding the woofer — defines the low-pass corner around 2 kHz. |
| C_lp (1.99×10⁻⁵ F ≈ 19.9 µF) | Capacitor across the woofer — completes the 2nd-order low-pass filter. |
| C_hp (1.99×10⁻⁵ F ≈ 19.9 µF) | Series capacitor feeding the tweeter — defines the high-pass corner at 2 kHz. |
| L_hp (0.00127 H) | Inductor across the tweeter — completes the 2nd-order high-pass filter. |
Together, those four parts form the textbook Linkwitz-Riley 12 dB/octave crossover.
Assistant / corrective networks
These parts do not carry the main audio signal but shape the response, impedance, and damping.
| Component | Function |
| Zobel Rz = 6 Ω, Cz = 13.9 µF | Impedance-equalization (R∥C) across the woofer to flatten its inductive rise. |
| Damper Rd = 10 Ω (∥ L_lp) | RC damper that lowers the Q of the low-pass section and smooths its knee. |
| Tweeter Rsh = 10 Ω | Shunt resistor across tweeter for impedance stabilization (part of an L-pad). |
| Notch Ln = 0.05 mH, Cn = 14 nF, Rn = 8 Ω | Series L-C-R “trap” across tweeter to suppress a breakup or resonance around 6 kHz. |
What the table shows overall:
● It differentiates the core filter (the main signal path) from the supporting “assistant” networks that refine the system without inserting extra components in series with the music signal.
● It quantifies how the “assisted” design adds carefully tuned corrective elements to improve phase accuracy, resonance control, and amplifier loading while maintaining a clean signal path.
In short, this table is the engineering recipe for the crossover—the electrical blueprint behind the plots used as Figures 1 and 2 (Figures at the top of this page).
1. What SPICE simulation means
SPICE stands for Simulation Program with Integrated Circuit Emphasis — a physicsbased circuit solver originally developed at UC Berkeley.
It computes how voltages and currents behave in a network of resistors, capacitors, and inductors across frequency.
In this case:
● The crossover components (L, C, R) were wired in the same topology used in a real speaker.
● SPICE equations solved the full complex impedance matrix for each frequency point (100 Hz → 20 kHz).
From that, the simulation produced:
● Total input current and voltage ratio (→ System Input Impedance graph)
2. How the table fits in
The table labeled “Crossover Components: Baseline and Assisted” lists every component value used in the SPICE netlist:
| Group | Role in Simulation |
| L_lp, C_lp, C_hp, L_hp | Main 2nd-order (12 dB/octave) crossover sections |
| Zobel Rz/Cz | Impedance equalizer across the woofer |
| Rd (∥ L_lp) | RC damper flattening woofer filter Q |
| Rsh | Tweeter impedance stabilizer |
| Ln/Cn/Rn | Tweeter resonance-notch filter |
Each numeric value (in SI units) was directly inserted into the SPICE equations to calculate the plots.
3. What the two plots represent
| Graph | What it Shows | How SPICE Calculated It |
| Electrical Transfer to Drivers | Output voltage delivered to woofer and tweeter vs frequency | Solved voltage divider equations across each branch |
| System Input Impedance | Total impedance seen by amplifier | Computed in Zin = V /from source node |
These are the exact quantities a real amplifier would see if it drove that network.
4. Why simulate
● Allows easy testing of “what-if” component changes.
● Reveals interactions between “in-path” and “assistant” elements.
In short:
● The table lists the component values used in that simulation.
● Together they represent a full, computer-modeled electrical analysis of your 2-way crossover design. It’s accurate enough that if you built it with those parts, the measured response would closely match the plots.
The simulated network is a two-way, 2nd-order (12 dB/octave) passive crossover, the classic Linkwitz–Riley or Butterworth topology used in countless loudspeakers.
Let’s break that down precisely:
1. Two-Way
That means it divides the audio signal into two frequency bands:
● High-pass section → Tweeter (handles treble)
No midrange driver is present — it’s a 2-driver system (woofer + tweeter).
2. Second-Order
Each branch has two reactive components (one L and one C), producing a 12 dB per octave slope:
| Section | Series Element | Shunt Element | Function |
| Woofer (low-pass) | Inductor (L_lp) in series | Capacitor (C_lp) in parallel across the woofer | Blocks highs above the crossover point |
| Tweeter (high-pass) | Capacitor (C_hp) in series | Inductor (L_hp) in parallel across the tweeter | Blocks lows below the crossover point |
At the crossover frequency (≈ 2 kHz in your case), both outputs are down by 6 dB, and their phase shift is complementary. When summed acoustically, they produce a flat overall response (the hallmark of a Linkwitz-Riley 2nd order, or LR2).
Secrets Sponsor
3. Assistant Networks (Supportive Elements)
To refine the behavior, four additional “off-path” corrective networks were included:
● RC damper (Rd∥L_lp) → reduces Q/ringing in low-pass
● Tweeter shunt resistor (Rsh) → stabilizes tweeter impedance
● Tweeter LCR notch (Ln–Cn–Rn) → suppresses tweeter resonance (~6 kHz)
These don’t change the fundamental 2nd-order topology; they fine-tune its accuracy.
4. Crossover Frequency and Behavior
Using the component values:
● C = 19.9μF
● Target load = 8 Ω
The electrical cutoff frequency is:
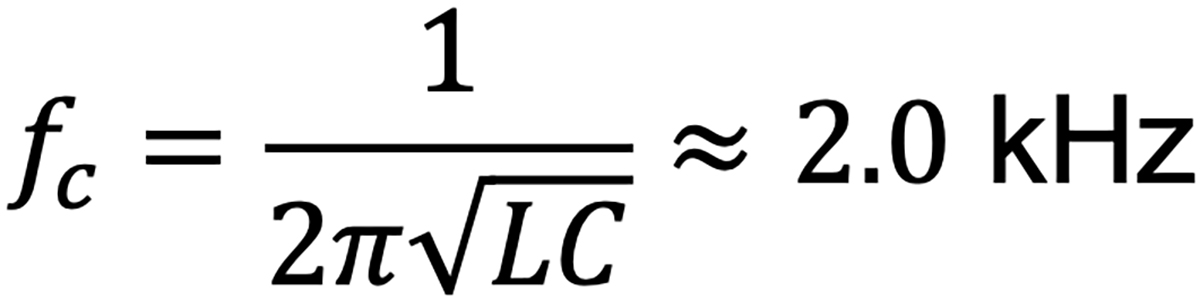
confirming a 2 kHz, 2nd-order crossover.
Summary
| Property | Description |
| System type | 2-way loudspeaker crossover |
| Order / Slope | 2nd-order (12 dB/octave per branch) |
| Topology | Linkwitz–Riley style (L-C mirrored) |
| Crossover frequency | ≈ 2 kHz |
| Drivers | Woofer + Tweeter |
| Assistant networks | Zobel, RC damper, shunt resistor, notch filter |
So, the network simulated in these graphs and table is a two-way, 2nd-order crossover, enhanced by auxiliary correction circuits that improve real-world performance without altering its fundamental LR2 (Linkwitz–Riley, 2nd-order) architecture.
It refers to a specific crossover alignment defined by Siegfried Linkwitz and Russ Riley, and it tells you how the filters are shaped, how steep they are, and how they sum.
A Linkwitz–Riley (LR) crossover is designed so that:
● The drivers are in phase at the crossover point
● The summed acoustic output has no peak or dip at the handoff
This is achieved by choosing specific filter Q values and mirror-image filter sections.
What the “2” in LR2 means
The number indicates the order of the filters:
● Electrical slope: 12 dB per octave per driver
● Each driver is –6 dB at the crossover frequency
So, for LR2:
● Tweeter: 12 dB/oct high-pass
● Both are –6 dB at fc
When summed acoustically:
That’s the defining LR behavior.
How LR2 differs from other common crossovers
| Type | Order | Level at Fc | Phase at Fc | Summation |
| Butterworth 2nd-order (BW2) | 2nd | –3 dB | 90° offset | +3 dB bump |
| Linkwitz–Riley 2nd-order (LR2) | 2nd | –6 dB | In phase | Flat |
| Linkwitz–Riley 4th-order (LR4) | 4th | –6 dB | In phase | Flat |
LR2 trades gentler slopes for excellent phase coherence.
Why LR2 matters in your crossover discussion
When I said:
“without altering its fundamental LR2 architecture.”
I meant:
● The auxiliary (‘assistant’) networks:
- Zobels
- notch filters
- damping resistors
- impedance stabilizers
These do not change the crossover order or alignment
So electrically and acoustically, it’s still an LR2 crossover, just better behaved in the real world.
Why LR2 is often chosen for high-end speakers
● Smooth power response
● Gentle slopes reduce stress on drivers
● Works well with well-behaved drivers and sophisticated correction networks
This fits perfectly with the YG Carmel 3 design philosophy: precision first, with driver and crossover behavior optimized through extensive simulation, and then implemented using carefully chosen passive components, rather than relying on brute-force filtering in the signal path.