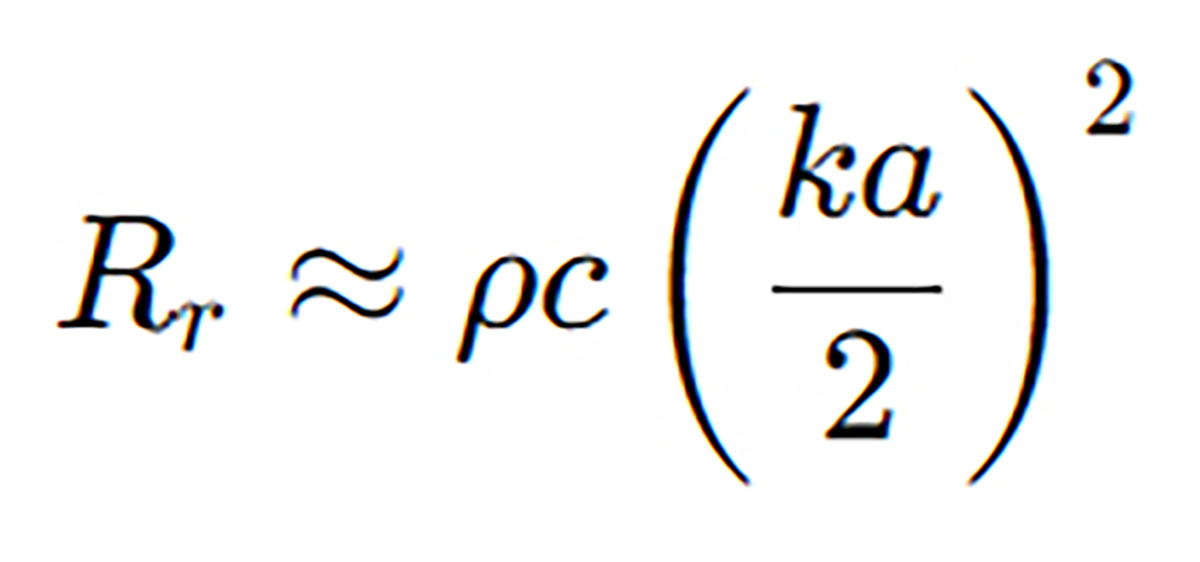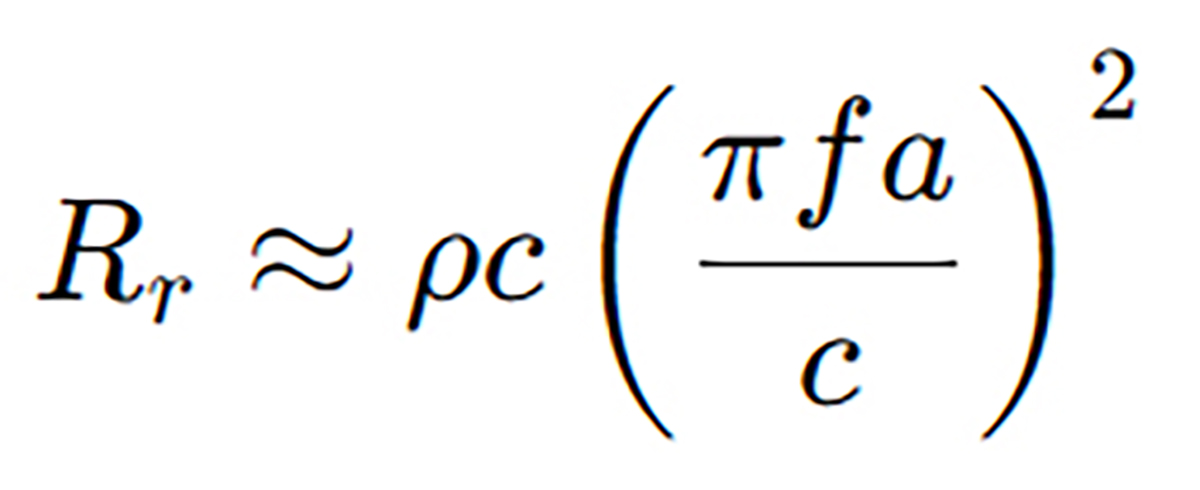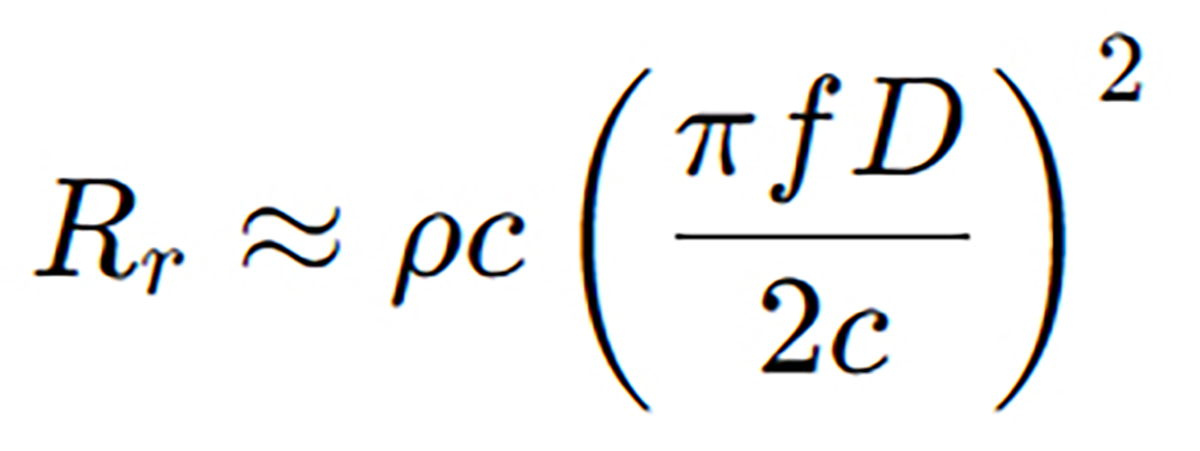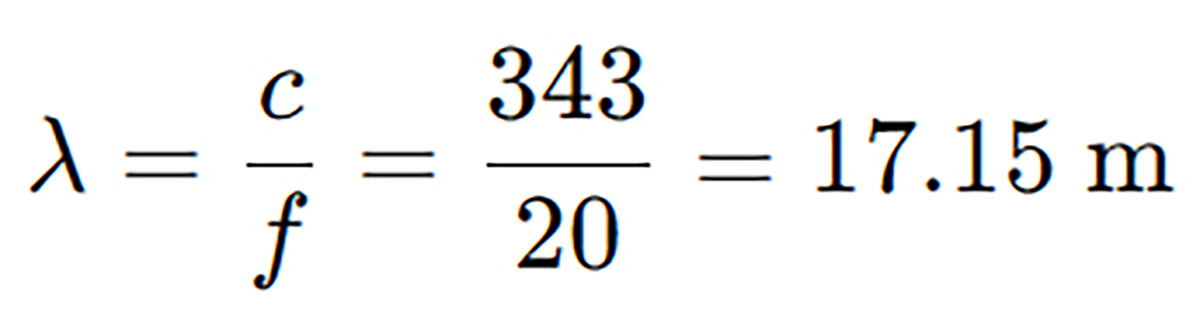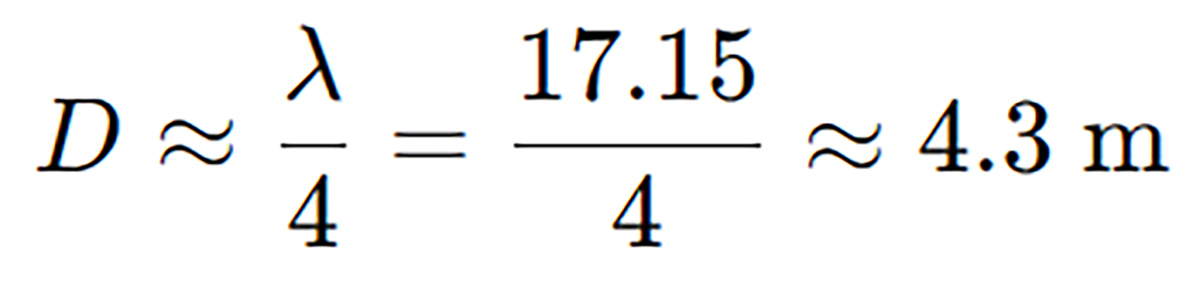The Concept of Radiation Resistance and Speaker Driver Diameter – Why Woofers Have to be Large

Radiation resistance is the portion of a speaker’s acoustical impedance that represents actual energy radiated into the surrounding air rather than being stored or reflected. This resistance is frequency-dependent and directly influenced by the size of the speaker diaphragm relative to the wavelength of the sound being produced.

At lower frequencies, where wavelengths are long, a small speaker struggles to effectively couple with the air, leading to low radiation resistance and poor efficiency. This is why woofers, which reproduce bass frequencies, must be larger than tweeters, which handle high frequencies with much shorter wavelengths. A speaker’s diameter determines how effectively it can transfer acoustic energy into its environment, with larger diameters increasing radiation resistance at low frequencies and improving efficiency.

The relationship between speaker size and radiation resistance can be described mathematically using wave propagation principles, particularly the wave number k and the speaker radius a. When the speaker diameter is small compared to the wavelength, most of the diaphragm’s motion results in near-field air displacement rather than far-field sound radiation. This mismatch leads to inefficient sound production at low frequencies unless a larger diaphragm is used. By understanding the principles of radiation resistance, speaker designers optimize the size of drivers to balance efficiency, frequency response, and power handling, ensuring high-fidelity audio reproduction across the entire sound spectrum.

• Definition: Radiation resistance is the part of a speaker’s impedance that represents the energy effectively transferred from the diaphragm to the surrounding air as sound.
• Frequency Dependence: At lower frequencies (bass), sound wavelengths are much longer, and a small diaphragm struggles to efficiently couple with the air due to low radiation resistance. This means a larger surface area is needed to effectively move enough air to produce audible bass.
• Efficiency: A woofer needs to be larger because a small driver would have to move much more (higher excursion) to displace the same amount of air as a large driver at low frequencies. A larger diaphragm increases radiation resistance, making low-frequency sound radiation more efficient.

Tweeters and Higher Frequencies

• Shorter Wavelengths: High frequencies have much shorter wavelengths, so even a small diaphragm has relatively high radiation resistance.
• Better Control: Smaller drivers can move quickly with minimal distortion, which is crucial for reproducing high-frequency details.

Thus, woofers are large to overcome low radiation resistance at low frequencies, while tweeters can remain small because they naturally couple well with air at high frequencies.

Radiation resistance in relation to speaker diameter and frequency involves acoustical impedance principles and wave propagation. The key concept is how efficiently a vibrating diaphragm couples with the surrounding air to radiate sound energy.

Acoustic Impedance Mismatch

• The acoustic impedance of free air is relatively low, while the speaker diaphragm has a much higher mechanical impedance.
• When the speaker is small relative to the wavelength, most of the speaker’s motion does not efficiently couple with the air, causing most of the energy to be stored as near-field motion instead of radiated as sound.

The Dipole Effect at Low Frequencies

• If the speaker is too small compared to the wavelength, the front and rear sound waves can partially cancel each other out (known as dipole cancellation or the “short-circuiting” effect).
• This further reduces efficiency and contributes to the small radiation resistance.

The Mathematics

1. Radiation Resistance Formula (Low-Frequency Approximation)

For a piston-like circular speaker in an infinite baffle, the radiation resistance R_r is approximated by:

where:

• ρ = air density (≈ 1.21 kg/m³ at room temperature),
• c = speed of sound in air (≈ 343 m/s),
• k = wave number, given by ,
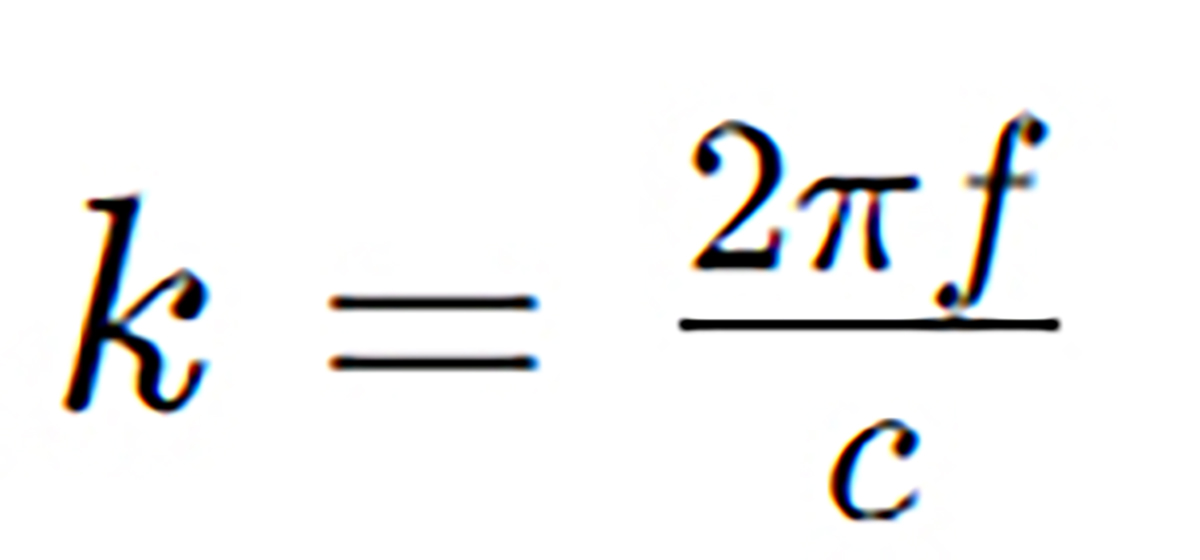• a = speaker radius (half of the diameter),
• ƒ = frequency in Hz.

Thus,

Or in terms of diameter D = 2a:

2. Frequency and Speaker Size Dependence

• At low frequencies (ka ≪ 1), meaning the speaker is small compared to the wavelength, radiation resistance is very small, and efficiency is low. The speaker struggles to transfer energy into the air.
• At higher frequencies (ka ≈ 1), efficiency increases, and the radiation resistance approaches a value where energy transfer is more effective.
• For effective bass reproduction, the speaker diameter should be a significant fraction of the wavelength λ = c/f, ideally D ≈ λ/4 or larger.

3. Practical Example

Let’s compare a woofer (12-inch) and a tweeter (1-inch) at different frequencies.

1. Woofer (D = 12 inches ≈ 0.3 m) at 50 Hz:

• λ=c/f=343/50=6.86m
• 
• Radiation resistance is very low → requires a large cone to move enough air.

2. Tweeter (D = 1 inch ≈ 0.025 m) at 5000 Hz:

• Λ=c/f=343/5000=0.0686m
• 
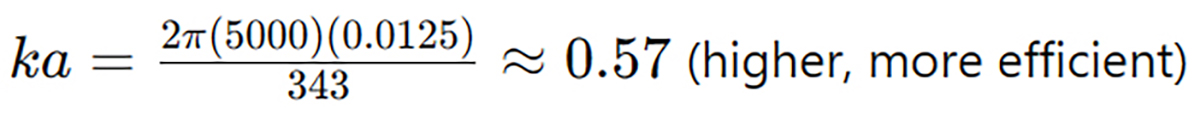
• Radiation resistance is much higher, so the small diaphragm efficiently radiates high frequencies.

Looking at radiation resistance from a different point of view, here are the calculations for the optimum woofer diameter for a 20 Hz signal, maximizing radiation resistance. (I have to say, though, that nobody will build one.)

To optimize radiation resistance for a woofer operating at 20 Hz, we need to consider the relationship between the baffle size, the wavelength of sound, and the piston diameter.

Step 1: Understanding the Wavelength

The wavelength (λ) of a 20 Hz sound wave in air (assuming speed of sound c = 343 m/s) is:

Step 2: Effective Woofer Diameter for Optimum Radiation Resistance

For optimal radiation resistance, the woofer should approach a size where its diameter is a significant fraction of the wavelength (typically 1/4 to 1/2 of the wavelength), but not so large that it becomes overly directional.

A good starting point is to ensure the piston diameter (D) is at least 1/4 wavelength:

That is a little over 14 feet in diameter!

This would be too large for a practical woofer, so we compromise by using a more realistic size while still maintaining efficient coupling to air.

Step 3: Practical Woofer Size Considerations

• In real-world loudspeaker design, subwoofers for 20 Hz operation typically range from 15 inches (38 cm) to 30 inches (76 cm) in diameter.
• A 24-inch (60 cm) woofer provides strong radiation efficiency without becoming impractically large.
• A cluster of smaller drivers (e.g., multiple 12-inch or 18-inch drivers in an array) can also approximate the effect of a single large piston.

Final Answer: Recommended Woofer Size

• A 24-inch (60 cm) woofer optimally balances radiation resistance and practical construction.
• If efficiency is a priority, an array of multiple 18-inch drivers can be used instead.

Keep in mind that a subwoofer this large is what you might hear in a commercial movie theater. It is not practical for home theaters, but it shows us why consumer subwoofers can be very large and with extremely powerful amplifiers in the thousands of watts. That’s what it takes to deliver strong, deep bass.

Bookshelf speakers with small woofers produce reasonable bass response, even with the radiation resistance problem. How do they do that?

The Problem: Radiation Resistance and Small Woofers

• Radiation resistance refers to the acoustic impedance that the air presents to a moving speaker cone.
• At low frequencies, the wavelength of sound is much longer than the diameter of a small woofer.
• Example: 50 Hz has a wavelength of about 6.8 meters (22 ft).
• Small woofers don’t “grab” the air efficiently at these wavelengths, which makes it hard to move enough air to create strong bass — this is the acoustic short-circuit problem in free air.

The Solutions: How Engineers Work Around This

1. Ported (Bass Reflex) Enclosures

• A tuned port reinforces the output at a certain bass frequency by using resonance.
• At the tuned frequency, the air movement from the port combines constructively with the woofer’s output.
• This increases the total bass output without needing more excursion from the driver.
• Downsides: potential for port noise or phase issues, but well-designed systems minimize these.

2. Sealed Enclosures + EQ (e.g., DSP)

• A sealed box gives tighter, faster bass, but rolls off more steeply.
• Modern designs (with built-in amplifiers) may use DSP (digital signal processing) to boost low frequencies, compensating for natural roll-off.
• This demands more power and excursion capacity, so these speakers rely on high-excursion drivers and powerful amps.

3. Room Reinforcement

• Rooms naturally reinforce bass via boundary effects, especially in corners or near walls.
• Small speakers are often tuned to take advantage of this, so their “on-paper” bass response isn’t the full story.

4. Passive Radiators

• A passive radiator (like a speaker cone without a magnet/voice coil) can replace the port.
• It behaves like a tuned port but with less port noise and potentially better low-end extension in a small box.

5. Driver Design Tweaks

• Small woofers can be made with:
• Longer voice coil gaps to allow more excursions.
• Stiffer surrounds and spiders to control excursion better.
• Strong magnets to maintain motor force over longer travel distances.

6. Adding Subwoofers

• The easiest solution to having small bass drivers in your speakers is to add a subwoofer. A 12” sub will probably suffice for stereo music listening, as most music does not contain 20 Hz material. For a home theater, if you watch a lot of action movies, consider getting the largest subwoofer that fits into your room. Let’s put it this way: In my home theater, I have two 16” subwoofers and a third subwoofer with two 12” drivers. Having a big subwoofer(s) is one of the most important ways of getting the sound that a commercial movie theater has.

The Trade-Offs

To get reasonable bass from a small speaker:

• Efficiency is sacrificed — you need more amplifier power.
• Maximum SPL is limited — physics still wins eventually.
• You might get distortion if you push it too far.
• Low-end extension is often exaggerated by a hump near the tuning frequency but rolls off fast below it.

Bookshelf speakers use a combo of tuned enclosures, smart driver design, DSP, and room acoustics to overcome the radiation resistance issue and produce usable bass, even though their woofers are too small to move air efficiently on their own at low frequencies.

The Reality

Marketing folks add about 1.5 inches for the surround, which is not part of the radiating diameter.

Regarding the equivalent size of multiple woofers, to find the equivalent radius, add the areas of each woofer together, then take the square root and divide by pi.

This equivalent woofer size calculation is dependent on knowing the actual cone size since the calculation must be made with that size.

For example, two 6.5-inch woofers are likely 5-inch woofers in terms of the actual cone diameter, which means the radius is 2.5 inches.  This gives 20 square inches of total cone area.

For three 6.5-inch woofers, the total cone area is 60 square inches. Take the square root of that and divide by pi to get the cumulative radius for the three woofers, which is 4.3 inches.

To determine the cumulative size, add 2(4.3) + 1.5, which equals 10.3 inches. Readers likely think they are getting a much bigger woofer with all those little ones, but they are not, mainly when the surround loss is accounted for.

Squaring a number is much more powerful than addition. A 6.5-inch woofer only has a 2.5-inch actual radius. A 12-inch woofer has a radius of 5.25 inches ((12″ – 1.5″)/2 = 5.25″). A 15-inch subwoofer with a 6.75-inch radius ((15 – 1.5)/2 = 6.75) may seem like a slight difference from the 12-inch woofer, but the area has increased from 27.6 square inches to 45.6 square inches. This is why I recommend getting the largest subwoofer you can fit into your home theater, and more than one if you can afford it.

• At lower frequencies, radiation resistance is small unless the speaker diameter is large.
• A woofer must be large because at low frequencies, a small diaphragm would require excessive movement (excursion) to displace enough air.
• A tweeter can be small because at high frequencies, radiation resistance is naturally higher.

This is why woofer sizes are larger than tweeters, to compensate for poor low-frequency radiation efficiency. As the saying goes, “There’s no replacement for displacement.”

REFERENCES

Beranek, Leo L. Acoustics. McGraw-Hill, 1954.

Morse, Philip M., and Ingard, K. Uno. Theoretical Acoustics. Princeton University Press, 1968.

Olson, Harry F. Acoustical Engineering. D. Van Nostrand, 1957.

Kinsler, Lawrence E., et al. Fundamentals of Acoustics. 4th ed., Wiley, 1999.

Rossing, Thomas D. Springer Handbook of Acoustics. Springer, 2007.

Thiele, Neville, and Small, Richard. Loudspeakers in Vented Boxes. Audio Engineering Society (AES) Papers, 1971.

M. A. Aarts and A. J. E. M. Janssen. Approximation of the Struve Function for Loudspeaker Modeling. Journal of the Acoustical Society of America, 2010.

H. Kuttruff. Room Acoustics. Taylor & Francis, 2009.

AES E-Library (Audio Engineering Society) – https://www.aes.org/e-lib/

Linkwitz Lab – https://www.linkwitzlab.com/

Rod Elliott’s Audio Pages (ESP) – https://sound-au.com/

Wikipedia – Acoustic Impedance – https://en.wikipedia.org/wiki/Acoustic_impedance