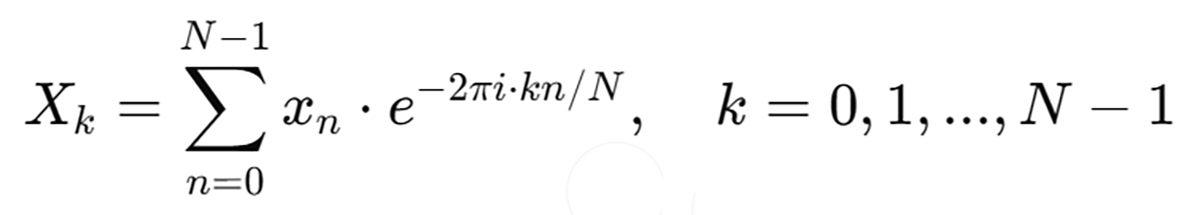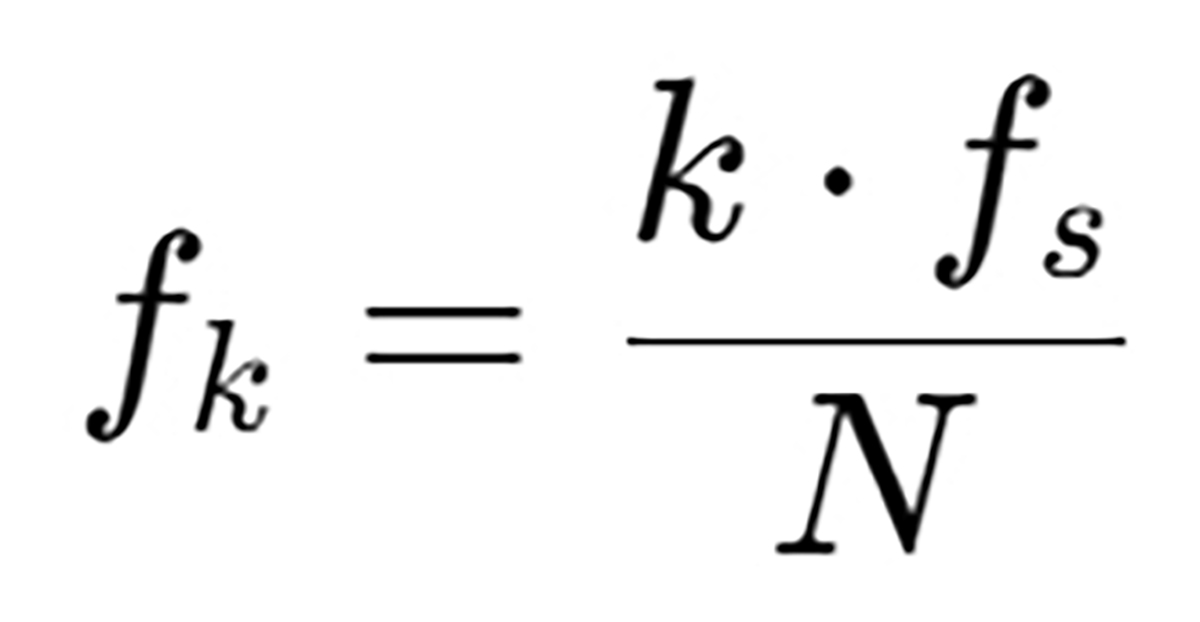Home
Up NextThe Concept of Radiation Resistance and Speaker Driver Diameter – Why Woofers Have to be Large
The Fast Fourier Transform (FFT) is applied to digital audio files in various scenarios, especially when analyzing or processing audio data.

Digital landscape orientation image of an abstract visualization of a sound wave spectrum, transitioning through red, orange, yellow, green, and blue hues from left to right against a dark background; The wave oscillates are visibly seen with varying amplitude and frequency

Introduction

The Fast Fourier Transform (FFT) is a foundational tool in digital audio analysis, enabling the decomposition of complex audio signals into their frequency components. At its core, FFT converts time-domain data, such as the amplitude variations in a digital audio file, into the frequency domain, revealing the spectral content of the sound. This transformation allows engineers, developers, and researchers to understand how energy is distributed across various frequencies, identify patterns or noise, and analyze tonal characteristics with precision. Whether for simple visualization in a spectrum analyzer or for advanced applications like equalization, compression, or restoration, FFT provides a mathematical bridge between what we hear and how audio is structured under the surface.

FFT analysis is applied to digital audio for both technical assessment and creative optimization. It enables detection of unwanted elements such as hiss, hum, or distortion artifacts, and it aids in quality control during mastering and production. In restoration work, FFT can isolate specific frequency bands where degradation has occurred, allowing for more surgical corrections. Moreover, audio codecs use frequency-domain data to implement perceptual compression, focusing on the frequencies most critical to human hearing. In music research and sound design, FFT reveals harmonic content, timbre, and transient behavior, offering insights that go far beyond what can be gleaned from waveform inspection alone. By transforming digital audio into a form that can be precisely measured and manipulated, FFT remains indispensable in virtually every corner of modern audio engineering.

Where FFT is Used

1. Audio Analysis

FFT is most commonly used to convert time-domain audio signals into the frequency domain, so we can see what frequencies are present in the sound.

  • Spectrograms: Visual representations of frequency content over time.
  • Pitch detection: Identifying musical notes or tuning instruments.
  • Timbre analysis: Understanding the tone, color, or texture of sound.

2. Audio Effects and Processing

FFT allows real-time manipulation of different frequency bands:

  • Equalization (EQ): Boosting or cutting specific frequency ranges.
  • Noise reduction: Identifying and removing unwanted frequencies.
  • Compression/Expansion: Dynamic range processing sometimes uses frequency-based info.
  • Reverb and Echo: Some reverbs analyze the frequency spectrum to apply effects more naturally.

3. Music Information Retrieval (MIR)

Used in tasks like:

  • Beat tracking: Identifying tempo and rhythmic elements.
  • Genre classification: Analyzing frequency patterns associated with different genres.
  • Chord recognition: Breaking down harmony based on frequency content.

4. Machine Learning & Audio AI

When training models on music/audio data:

  • FFT or STFT (Short-Time Fourier Transform) is often applied to extract features like Mel-frequency cepstral coefficients (MFCCs) or spectral contrast, which are then fed into neural networks.

So, when does this actually happen on a file level?

  • Not directly to the *.mp3 or *.wav file.
  • The file is decoded into raw audio data (PCM) first.
  • Then the FFT is applied to chunks of the waveform (typically 512, 1024, or 2048 samples at a time).

Secrets Sponsor

The Mathematics of FFT Analysis

The mathematics behind FFT is all about efficiently computing the Discrete Fourier Transform (DFT), which lets you convert signals from the time domain (how they change over time) into the frequency domain (what frequencies are present).

1. Discrete Fourier Transform (DFT)

Suppose you have a signal sampled as N values:

Discrete Fourier Transform (DFT) mathematical equation

The DFT of that signal is:

Discrete Fourier Transform (DFT) signal mathematical equation

  • Xn: the time-domain samples
  • Xk: the complex frequency components (amplitude + phase)
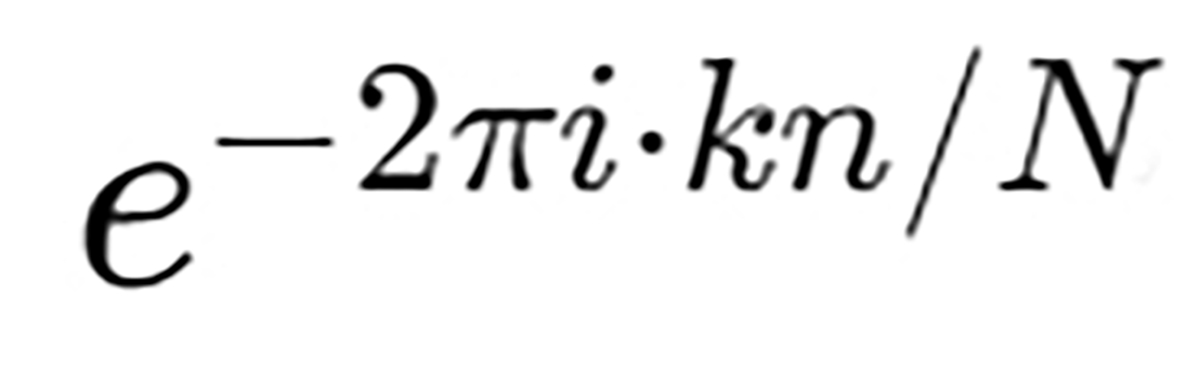  • Complex sinusoids (basis functions) mathematical equation: complex sinusoids (basis functions)
  • K: the index of frequency components

You can think of this as projecting your signal onto sine and cosine waves of different frequencies.

2. FFT: Fast Fourier Transform

DFT is computationally expensive: O(N2) operations.

FFT is a clever algorithm (like the Cooley–Tukey algorithm) that reduces it to O(N2) by exploiting symmetry and periodicity in the complex exponentials.

So, FFT gives the same result as DFT, just faster.

3. What Do the FFT Results Mean?

Each Xk gives:

  • Magnitude: ∣ Xk ∣ = how strong this frequency is
  • Phase: arg(Xk ) = phase shift of that frequency component

To get real frequency values:

FFT: Fast Fourier Transform mathematical equation

Where:

  • fs: sampling rate
  • N: number of samples
  • k: index

Example: Audio at 44.1 kHz

If your signal is sampled at 44,100 Hz (CD quality), and you take an FFT of 1024 samples:

  • Frequency resolution = FFT: Fast Fourier Transform frequency response mathematical equation
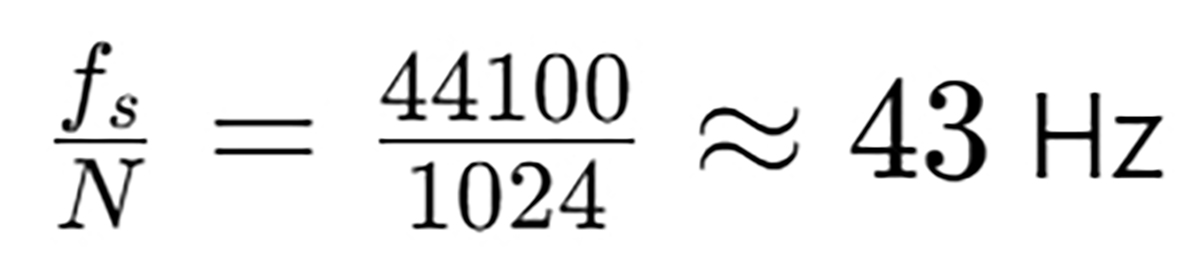
  • FFT will output 1024 bins, representing frequencies from 0 to ~22,050
  • You usually only look at the first half (0 to Nyquist frequency)

Summary

  1. FFT is just a fast way to compute DFT.
  2. It reveals what frequencies are present and how strong they are.
  3. It’s based on summing up weighted sinusoids across the signal.

Secrets Sponsor

Conclusions

Fast Fourier Transform (FFT) analysis plays a crucial role in understanding and interpreting digital audio files. By transforming time-domain waveforms into the frequency domain, FFT allows us to see the underlying frequency components that make up a sound. This is essential for a wide range of audio applications, from music production and audio engineering to speech analysis and audio forensics. Whether analyzing pitch, detecting harmonics, removing noise, or creating audio effects, FFT provides the mathematical foundation for revealing the spectral content that defines a sound’s character and quality.

The importance of FFT in digital audio cannot be overstated. It enables both machines and humans to make sense of complex audio data in a way that is efficient, accurate, and insightful. As digital audio continues to evolve, FFT remains at the core of modern signal processing, powering tools for visualization, transformation, and feature extraction. Its ability to dissect sound into its fundamental frequencies makes it indispensable in any serious analysis or manipulation of digital audio content.

REFERENCES

  1. Oppenheim, A. V., & Schafer, R. W. (2009). Discrete-Time Signal Processing (3rd ed.). Prentice Hall.
  2. Smith, Julius O. (2007). Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications. W3K Publishing.
  3. Brigham, E. O. (1988). The Fast Fourier Transform and Its Applications. Prentice Hall.
  4. Lyons, R. G. (2010). Understanding Digital Signal Processing (3rd ed.). Prentice Hall.
  5. Proakis, J. G., & Manolakis, D. G. (2006). Digital Signal Processing: Principles, Algorithms, and Applications (4th ed.). Pearson.
  6. Rabiner, L. R., & Gold, B. (1975). Theory and Application of Digital Signal Processing. Prentice Hall.
  7. Allen, J. B., & Rabiner, L. R. (1977). “A Unified Approach to Short-Time Fourier Analysis and Synthesis.” Proceedings of the IEEE, 65(11), 1558–1564.
  8. Smith, Julius O. (2008). “Spectral Audio Signal Processing, https://ccrma.stanford.edu/~jos/sasp/